The Principle of Absence of Arbitrage

Exploring the principle of absence of arbitrage, its applications in asset valuation, and its impact on market efficiency.

The principle of absence of arbitrage is a cornerstone of modern finance and asset valuation. It states that no risk-free profit opportunities can exist in an efficient market. In other words, if two assets provide the same future cash flows, they must be valued at the same price; otherwise, a risk-free profit could be made, which contradicts market efficiency.

1. Definition of Arbitrage

Arbitrage refers to a strategy that exploits price differences of the same asset or equivalent assets in different markets to make a risk-free profit without an initial investment.

Simple Example

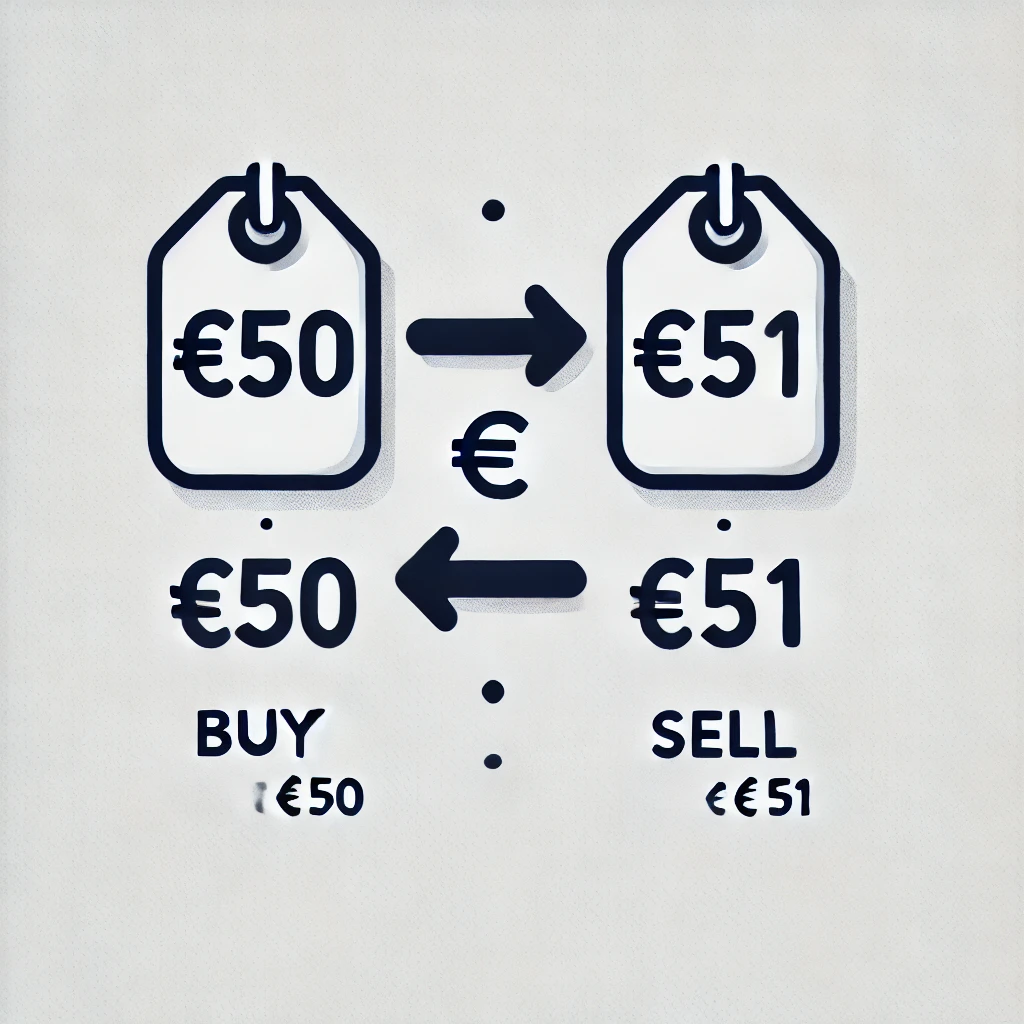
• Suppose a stock is priced at €50 on the Paris Stock Exchange and €51 on the London Stock Exchange.
• An arbitrageur could buy the stock in Paris at €50 and sell it simultaneously in London at €51, making a €1 risk-free profit per share.
• In a competitive and efficient market, such opportunities should not exist or last only briefly.

2. The Law of One Price (LoOP)

The absence of arbitrage leads to the Law of One Price (LoOP), which states:

“Two assets that generate the same future cash flows must have the same price today.”

If violated, arbitrageurs could buy the underpriced asset and sell the overpriced one until their prices converge.

Example of the Law of One Price

• Suppose a government bond and a derivative product on that bond offer the exact same future payments.
• If the bond sells for €100 and the derivative for €98, an investor could buy the derivative and sell the bond to generate a risk-free profit.
• The demand for the derivative would then push its price up to €100, eliminating the arbitrage opportunity.

3. Applications in Asset Valuation

The principle of absence of arbitrage is fundamental in pricing financial assets:

a) Bonds and Stocks

• Their prices should reflect the discounted value of future cash flows; otherwise, arbitrage opportunities arise.

b) Derivatives (Options, Futures, Swaps, etc.)

• Pricing models like Black-Scholes for options or futures pricing models ensure arbitrage-free relationships between derivatives and underlying assets.

c) Foreign Exchange Markets

• Purchasing Power Parity (PPP) and Interest Rate Parity (IRP) ensure that exchange rates adjust to prevent arbitrage opportunities across currencies.

d) Investment Portfolios

• Modern finance theories like CAPM (Capital Asset Pricing Model) and Arbitrage Pricing Theory (APT) assume that excess returns require additional risk and arbitrage cannot generate abnormal profits.

4. Implications of the Absence of Arbitrage Principle

a) Market Efficiency

• In a market where arbitrage is impossible, asset prices incorporate all available information, making it difficult to achieve abnormal profits.

b) Market Regulation and Surveillance

• Financial authorities monitor markets to prevent illegal arbitrage practices that could create market distortions (e.g., price manipulation).

c) Financial Product Development

• Banks and hedge funds use sophisticated strategies to exploit temporary inefficiencies, known as statistical arbitrage.

5. Limitations and Exceptions

a) Arbitrage Limited by Transaction Costs

• In reality, transaction costs (brokerage fees, taxes, bid-ask spreads) may prevent pure arbitrage from being profitable.

b) Informational Arbitrage

• Some investors (hedge funds, high-frequency traders) may spot price discrepancies before others, making arbitrage accessible only to those with informational or technological advantages.

c) Illiquid Markets

• In low-liquidity markets, assets may have different prices temporarily because there are not enough trades to correct price anomalies quickly.

Conclusion

The principle of absence of arbitrage is essential in finance as it ensures assets are fairly valued and markets remain efficient. It leads to the Law of One Price, which dictates that identical or equivalent assets must have the same price. This principle is widely used in valuing stocks, bonds, derivatives, and exchange rates. However, real-world factors like transaction costs, liquidity constraints, and information asymmetry may sometimes limit arbitrage opportunities.

References

• Fama, E. F. (1970). “Efficient Capital Markets: A Review of Theory and Empirical Work.” The Journal of Finance.
• Black, F., & Scholes, M. (1973). “The Pricing of Options and Corporate Liabilities.” Journal of Political Economy.
• Ross, S. A. (1976). “The Arbitrage Theory of Capital Asset Pricing.” Journal of Economic Theory.
• Hull, J. (2017). “Options, Futures, and Other Derivatives.” Pearson.
• CFA Institute. (n.d.). “Principles of Arbitrage-Free Pricing.” Retrieved from CFA Institute